Numerical Differentiation Python Implementation

John Bryan

• Sections
  • Equations
    • Central Difference, Richardson Extrapolation, et al
    • Chebyshev Differentiation Matrix
    • Complex Step Differentiation
  • Python Implementation
  • Results
    • Central Difference, Richardson Extrapolation, et al
    • Chebyshev Differentiation Matrix
    • Complex Step Differentiation
      
      
  
  
  
• Equations
  
  
  • Central Difference, Richardson Extrapolation, et al
    
    
    • Central Difference, \begin{equation} f'(x) \approx \frac{f(x+h)-f(x-h)}{2h} \end{equation}
    • Second derivative, \begin{equation} f''(x) \approx \frac{f(x+h)-2f(x)+f(x-h)}{h^2} \end{equation}
    • Richardson extrapolation, \begin{equation} f'(x) \approx \frac{f(x+\frac{h}{2})-f(x-\frac{h}{2})}{h} +\frac{1}{3} \left[ \frac{f(x+\frac{h}{2})-f(x-\frac{h}{2})}{h} - \frac{f(x+h)-f(x-h)}{2h}\right] \end{equation}
    • Nonsymmetric Difference, \begin{equation} f'(x) \approx \frac{-3f(x)+4f(x+h)-f(x+2h)}{2h} \end{equation}
    • Five-point method, \begin{equation} f'(x) \approx \frac{-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)}{12h} \end{equation}
    • Letting r.h.s. of previous equation equal U(h), \begin{equation} f'(x) \approx \frac{16U(h)-U(2h)}{15} \end{equation}
  • Chebyshev Differentiation Matrix
    
    
    • Number of Chebyshev nodes = n+1
      
      
    • Chebyshev nodes \begin{equation} x[k]=\cos(k\pi/n),\qquad 0 \le k \le n \end{equation}
    • Endpoint coefficients, \begin{equation} c_i= \begin{cases} 2, & i = 0,n \\[8pt] 1, & 1 \le i \le n-1 \\ \end{cases} \end{equation}
    • Chebyshev differentiation matrix D elements, \begin{equation} D[i,j]= \begin{cases} (-1)^{i+j}\dfrac{c_i}{c_j(x[i]-x[j])} , & i \ne j , i+j \le n \\[10pt] -D[n-i,n-j] , & i \ne j, i+j \gt n \\[10pt] \displaystyle -\sum_{j=0,\; j \ne i}^{n}D[i][j], & i=j \end{cases} \end{equation}
    • With a,b domain endpoints, \begin{equation} x=a+0.5(b-a)(x+1) \end{equation} \begin{equation} D[i,j]=\frac{2 \cdot D[i,j]}{b-a} \end{equation}
    • First derivative \begin{equation} y' \approx Dy \end{equation}
    • Second derivative \begin{equation} y'' \approx Dy' \end{equation}
  • Complex Step Differentiation
    
    
    • First derivative, \begin{equation} f'(x) \approx \frac{\Im(f(x+ih)}{h} \end{equation}
    • Second derivative, \begin{equation} f''(x) \approx \frac{2}{h^2}[f(x)-\Re\{f(x+ih)\}] \end{equation}
• Python Implementation.
  
  
• Results
  
  
  • Central Difference, Richardson Extrapolation, et al Results
    
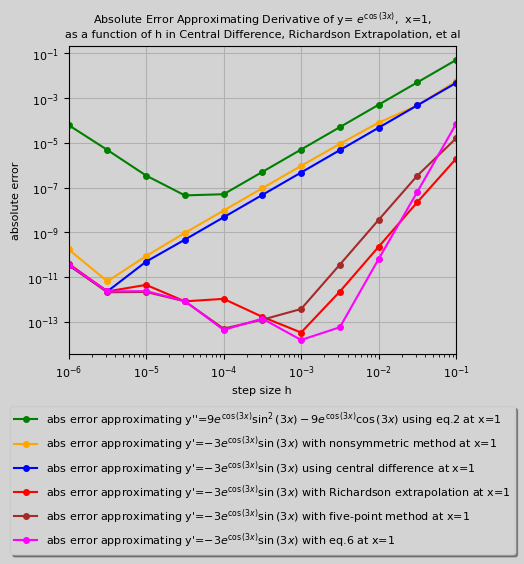
  • Chebyshev Differentiation Matrix Results
    
    
    
    
    
    
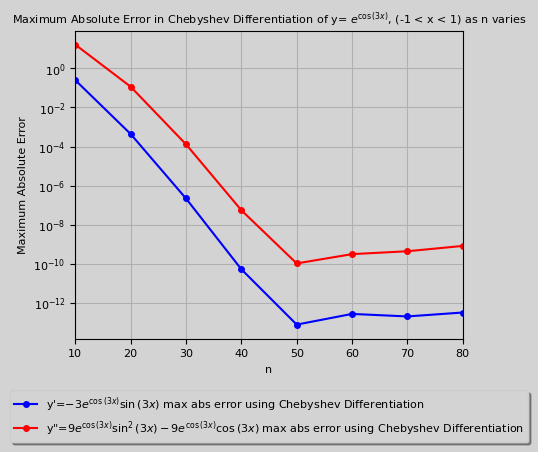
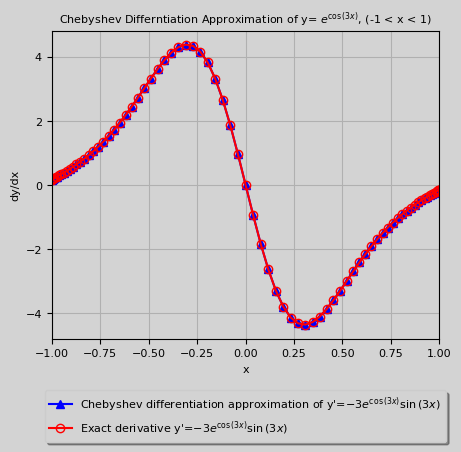
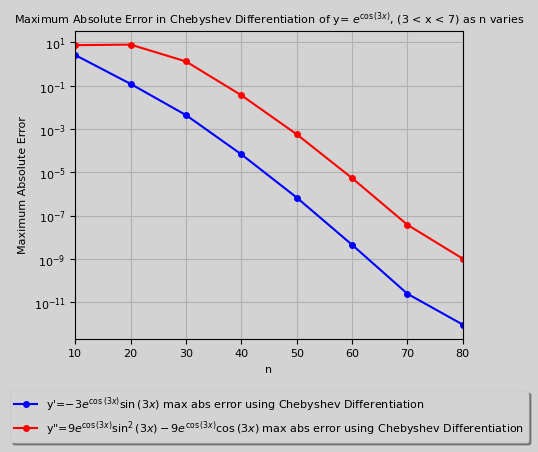
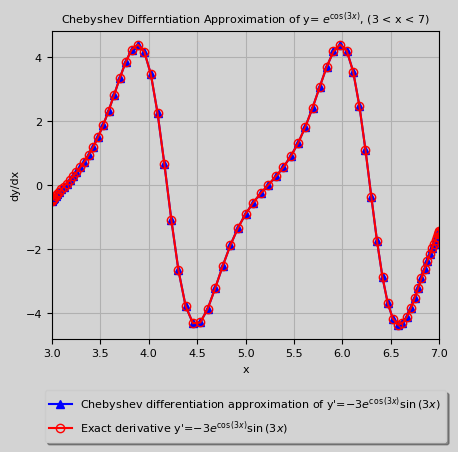
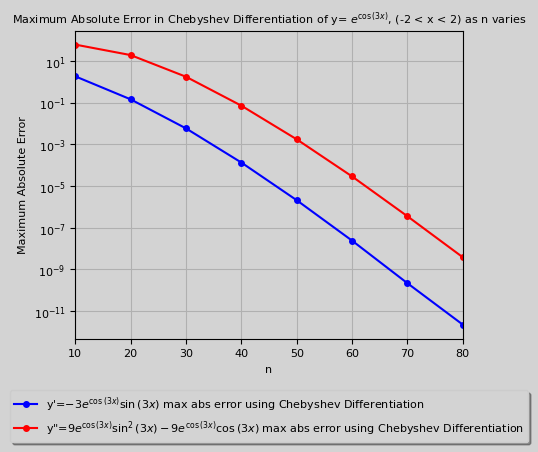
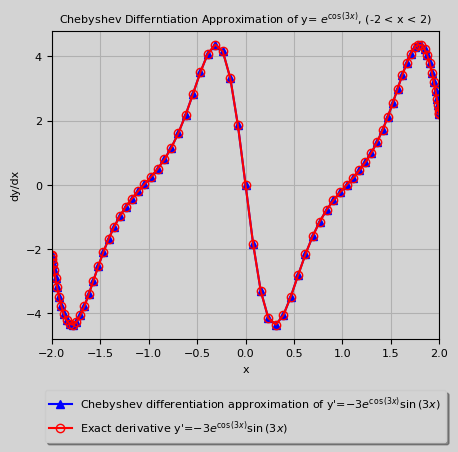
  • Complex Step Differentiation Results
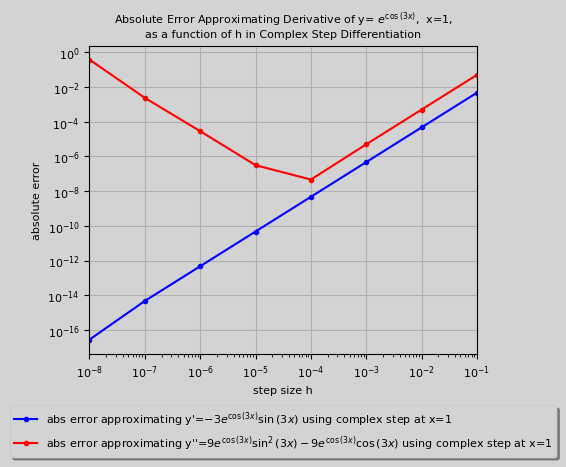